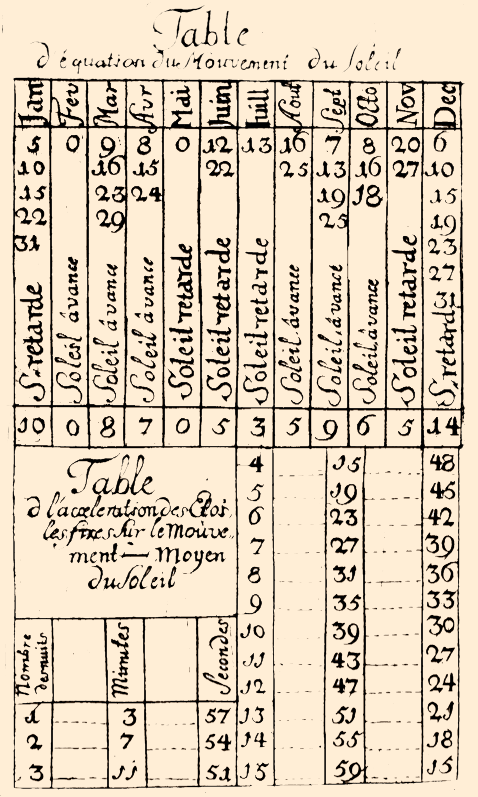
Tables d'équation
On appelle "équation de temps" la différence entre le temps Vrai et le temps Moyen, et "Tables d'Equations" les listes dressées par les astronomes indiquant pour tous les jours de l'année cette différence.
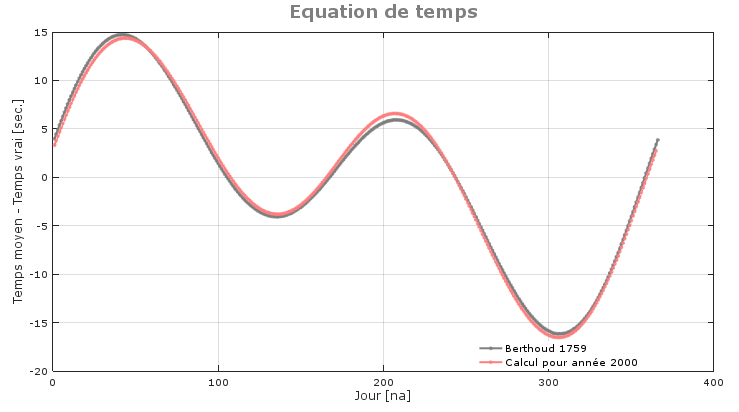
Equation de temps pour l'année 2000 (rouge) ainsi que celle publiée par Berthoud en 1759 (gris)
Les deux composantes de l'équation de temps
Si l'on décompose la courbe de l'équation de temps pour visualiser ces deux composantes on observe:
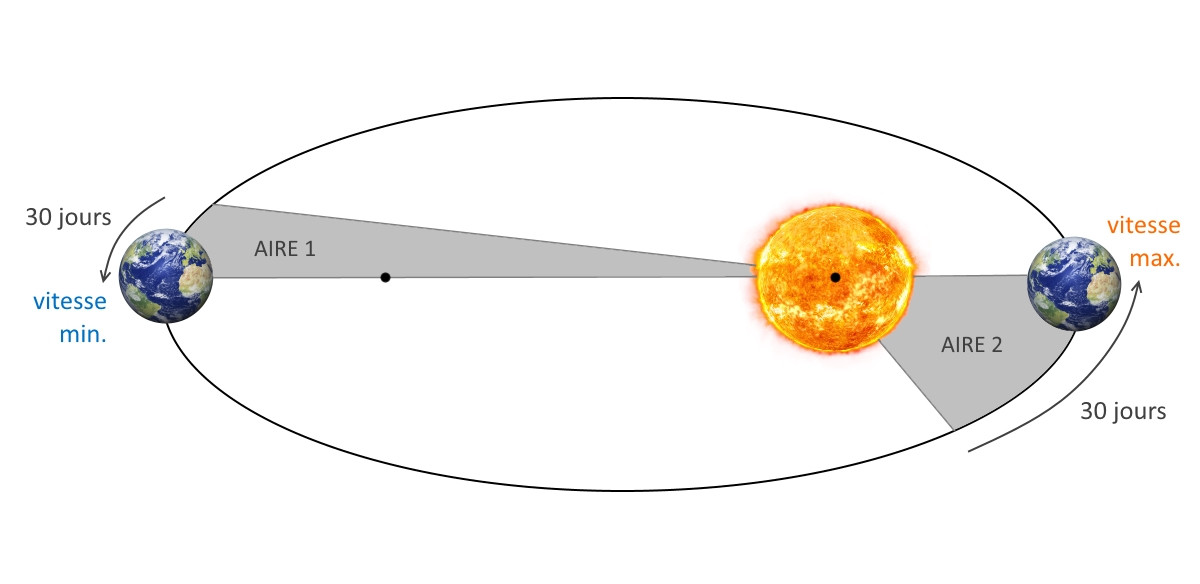
- L'influence de la trajectoire elliptique de la Terre autour du soleil (appelée équation du centre)
Cette contribution a la forme d'une ondulation qui s'annule deux fois par année, lorsque la Terre passe au périhélie (point le plus proche du soleil) et à l'aphélie (point le plus éloigné). Entre ces deux points elle passe par un extrémum (un maximum et un minimum par année)
- L'influence de l'inclinaison de l'axe de rotation de la Terre sur l'écliptique (appelée réduction à l'équateur).
Cette contribution présente deux ondulations par année, passant chacune par un maximum et un minimum. Plus précisément les maximums apparaissent aux solstices d'hiver et d'été et les minimums aux équinoxes.
Les schémas ci-dessous permettent de visualiser cette contribution.
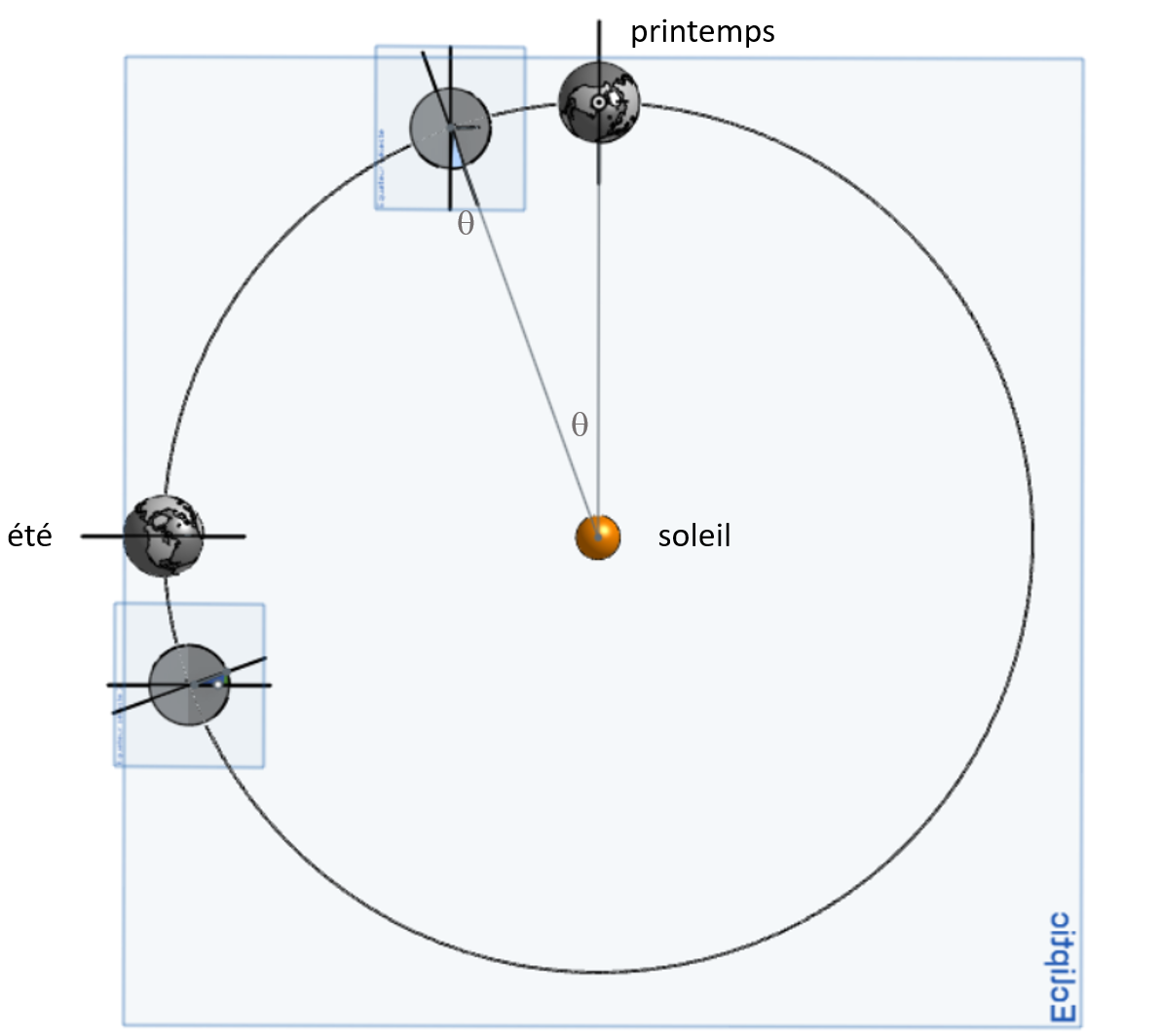
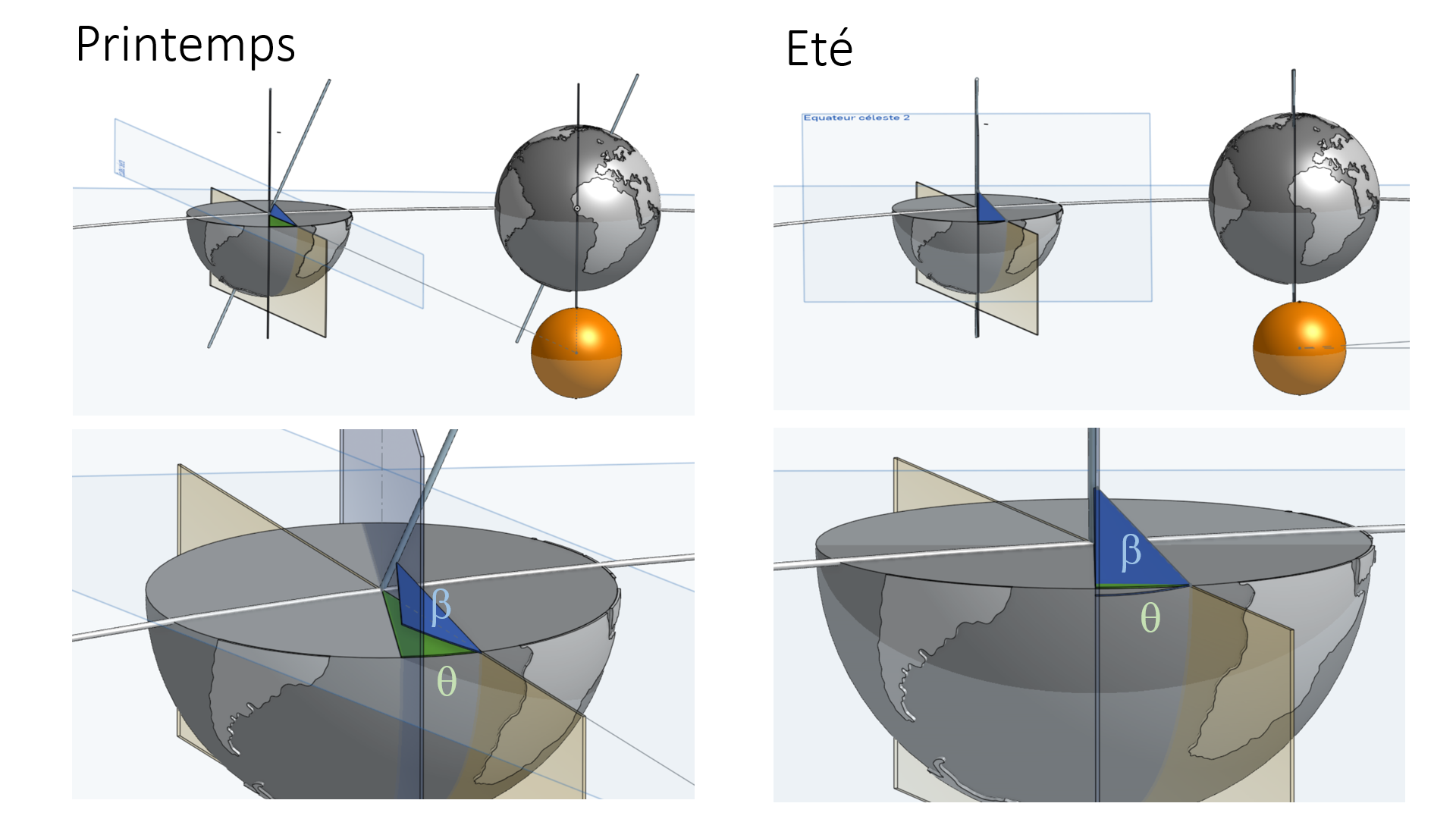
Schéma représentant la Terre à 1 jour d'intervalle dans deux situations extrêmes, à l'équinoxe de printemps et au solstice d'été. Les proportions et angles sont exagérés afin de faciliter la visualisation.
A un jour d'intervalle la Terre c'est déplacée sur son orbite d'un angle θ, en plus de faire un tour complet par rapport aux étoiles lointaines (représenté par les deux plans parallèles bleus) le globe doit encore faire un angle (correspondant à θ dans le plan de l'écliptique [section triangulaire verte]) afin de compléter la journée et ramener le soleil au zénith (plans jaunes).
Comme la Terre ne tourne pas dans le plan de l'écliptique mais autour de son axe incliné à 23.43° par rapport à l'écliptique, l'angle de rotation β (section triangulaire bleue) est alors différent de θ (section triangulaire verte).
Cette différence varie au cours de l'année, elle est maximale aux équinoxes et minimale aux solstices.
Les deux contributions s'additionnent pour générer la courbe caractéristique, en vague descendante, de l'équation de temps.
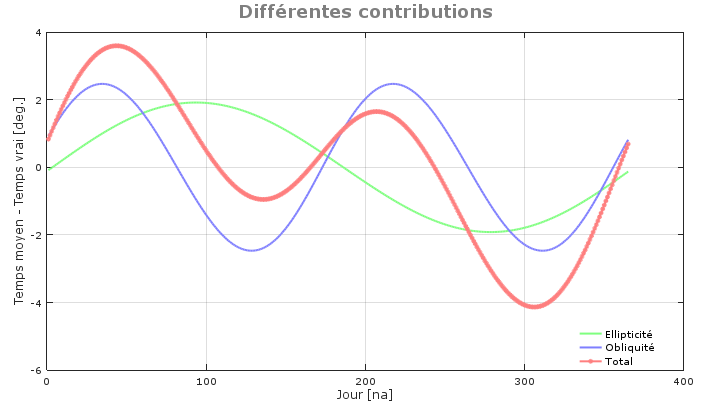
Les deux composantes de l'équation de temps: ellipticité de l'orbite terrestre (vert) et obliquité de son axe de rotation (bleu).
Evolution séculaire
Perturbation sur la composante elliptique
L'interaction Terre/Lune/Soleil génère un mouvement circulaire de l'axe de rotation de la Terre autour de la perpendiculaire à l'écliptique (plan dans lequel s'inscrit l'orbite terrestre). Cette rotation s'effectue sur un cycle qui dure environ 25'760 ans.
Pour décrire ce phénomène plus précisément, commençons par la définition des équinoxes. L'inclinaison de l'axe de rotation de la Terre détermine les équinoxes, il s'agit des positions sur l'orbite où la projection de l'axe de rotation de la Terre et le vecteur Terre-Soleil sont à 90°.
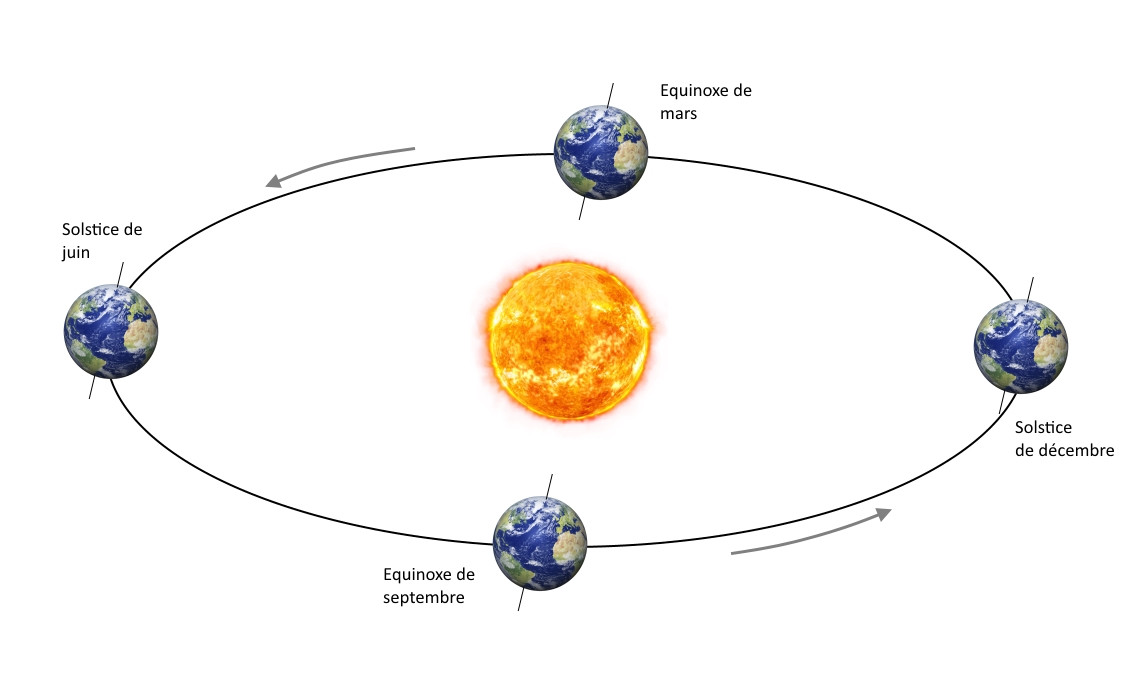
Equinoxes, solstice et mouvement de précession de l'axe de rotation de la Terre.
Ce pivotement de l'axe de rotation de la Terre qui se déroule sur une période de 25'760 ans entraîne donc un déplacement des points d'équinoxes sur l'orbite terrestre. Ce déplacement se fait dans le sens opposé au sens de rotation de la Terre sur son orbite.
Par conséquent, chaque année les équinoxes se produisent sur un point de l'orbite situé avant la réalisation d'un tour complet, d'où le nom donné à ce phénomène: précession des équinoxes.
Pour être encore plus précis, cette avance correspond à 50,2 sec. d'arc sur l'orbite terrestre. Il faudra compter encore 20 minutes pour que la Terre parcoure ces 50,2 sec. d'arc et termine son tour complet (année sidérale).
La vidéo ci-dessous consacrée aux caractéristiques de l'orbite terrestre permet de visualiser le phénomène:
Vidéo - Précession des équinoxes
Au niveau de la courbe de l'équation de temps, la précession des équinoxes provoque un décalage sur l'axe horizontal de la composante liée à l'ellipticité.
Perturbation sur la composante inclinaison
A cette évolution moyenne de la direction de l'axe de rotation de la Terre liée à la précession des équinoxes on ajoute des altérations sur sur la valeur de son angle d'inclinaison.
A long terme, sur une période de 41'000 ans, on observe une évolution séculaire de l'inclinaison de l'écliptique entre 21,6° et 24,4°.
D'autre part, à très court terme, les oscillations du plan de l'écliptique lunaire génèrent un petit mouvement elliptique de l'axe de rotation terrestre autour de son cercle moyen de précession. Ce mouvement, appelé nutation, a été mis en évidence en 1748 par James Bradley et il s'effectue sur une période de 18,7 ans.
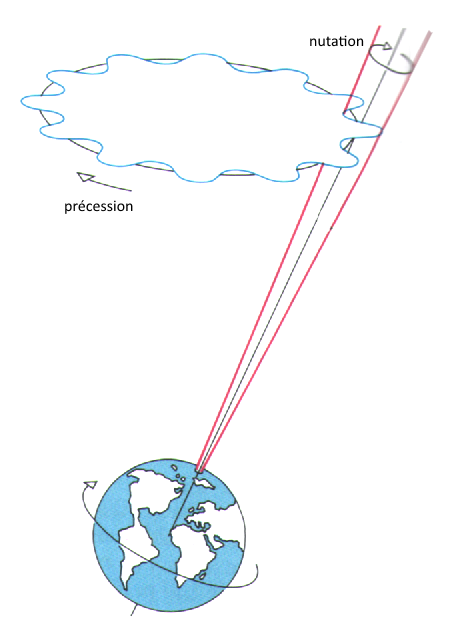
Nutation de l'axe de rotation terrestre
La conséquence de ces perturbations se résume en une modification de l'obliquité qui caractérise l'inclinaison de l'axe de la Terre par rapport à lécliptique.
Au niveau de la courbe de l'équation de temps ces perturbations se traduisent par une variation de l'amplitude et un petit décalage horizontal de la composante liée à l'obliquité.
Si l'on représente sur un graphique tridimensionnel l'évolution de la courbe de l'équation de temps pour les 10'000 années à venir on obtient, en première approximation, la surface ci-dessous:
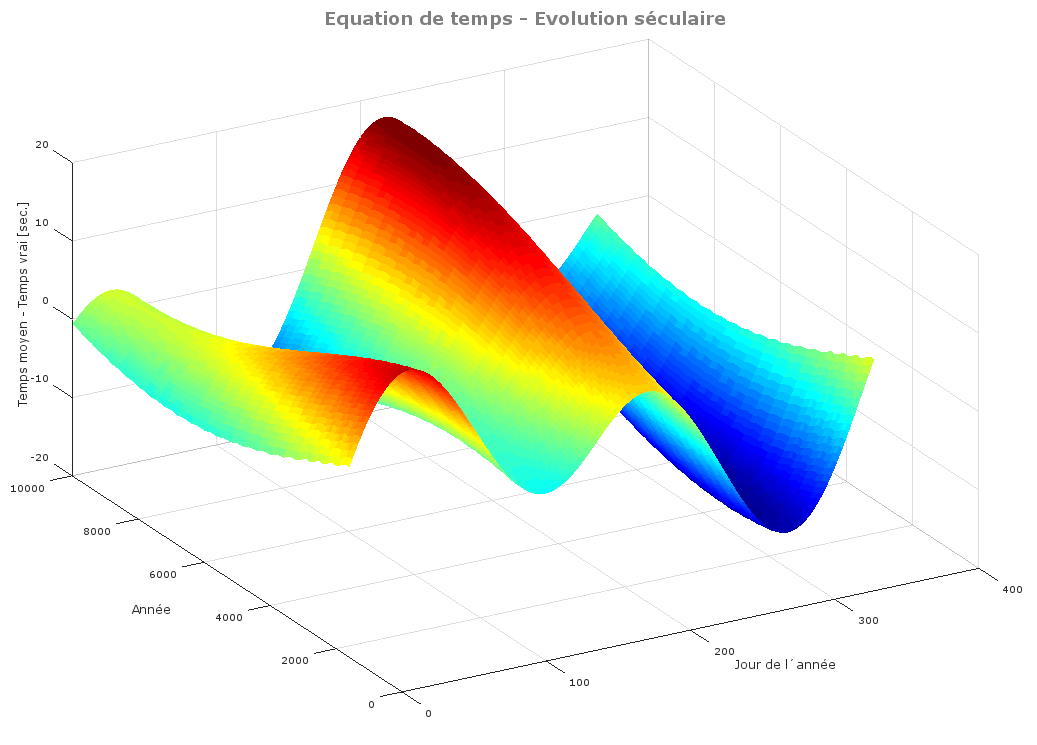
Evolution séculaire de l'équation de temps
Autres perturbations
Au-delà de la précession des équinoxes, de la nutation et de l'évolution séculaire de l'inclinaison de l'écliptique dont nous avons parlé ci-dessus, le mouvement du globe comporte encore de nombreuses complexités dues aux effets combinés de la lune, du soleil et des autres planètes.
En particulier l'ellipse qui représente l'orbite terrestre pivote autour du soleil avec une période de 21'000 ans lorsque l'on se réfère au repère des étoiles lointaines. De plus, son excentricité varie (l'ellipse s'aplatit plus ou moins) entre 0 et 5,3 dans une période de 100'000 ans. La valeur actuelle de l'excentricité est de 1,67.
Pendules et montres à équation
Lorsqu'une pendule ou une montre indique l'heure vraie, en plus de l'heure moyenne, alors on parle de pendule ou montre "à équation". Il existe plusieurs principes d'affichage de l'équation de temps, nous les présenterons dans un article à venir.
Utilité
Aujourd'hui l'équation de temps apparaît comme une complication sans véritable utilité, cependant jusqu'au XXème siècle elle présentait un véritable intérêt. En effet elle permet de régler une montre sur le soleil (temps vrai) sans avoir recours aux tables d'équation publiées par les astronomes.
Régler une montre à l'époque de Sully ou Berthoud n'était pas une opération aisée, c'est l'apparition de la radio qui a permis de simplifier cette opération en diffusant une référence horaire à large échelle. Sinon il fallait se baser sur l'horloge d'un clocher, une pendule de référence ou éventuellement un cadran solaire associé aux tables d'équation.
Question du signe
La littérature et les applications horlogères ne considèrent pas toujours l'équation de temps avec la même convention de signe.
Dans les publications françaises, l'équation de temps est généralement exprimée sous la forme "temps moyen - temps vrai".
Donc si l'équation de temps est positive le soleil est en retard sur le temps moyen.
Par contre au Royaume-Uni, aux Etats-Unis ou en Belgique les auteurs ont utilisé généralement la forme "temps vrai - temps moyen".
Donc si l'équation de temps est positive le soleil est en avance sur le temps moyen.
Certains auteurs, dont Ferdinand Berthoud, ne mettent pas de signe dans les tables qu'il a publiées. Par contre ils indiquent "soleil en retard" ou "soleil en avance" afin de clarifier l'interprétation des valeurs numériques relevées.
Ce joyeux méli-mélo dans les écrits au cours des siècles a également engendré des indictions de cadran qui ne sont pas correctes chez les horlogers. L'équation de temps reste une complication dont l'interprétation nécessite un peu d'entraînement!
Dossier: Equation de temps