Alliages invariables
Anomalie de la dilatation thermique des alliages fer/nickel
Au Bureau International des Poids et Mesures (BIPM) à Sèvre près de Paris, Charles-Edouard Guillaume (voir encadré) est en charge de trouver une alternative pour les règles-étalons de second ordre (d'usage courant dans les laboratoires et dans l'industrie). Ces étalons étaient alors fabriqués dans un alliage de platine/iridium développé par Henri Sainte-Claire-Deville et qui avait l'avantage d'une grande dureté, de résister aux agressions chimiques et de présenter un faible coefficient de dilatation thermique. Cependant le platine/iridium (appelé aussi platine iridié) était cher et très rare, et ne pouvait pas raisonnablement servir de standard pour fournir les laboratoires et l'industrie du monde entier en mètres étalons.
En étudiant les travaux de John Hopkinson, physicien anglais spécialiste du magnétisme, ainsi que ceux de J.R. Benoît, directeur du BIPM, il découvre la famille des alliages constitués de fer et de nickel. Ces alliages présentent des anomalies intéressantes au niveau de leur coefficient de dilatation thermique.
Les fonderies Commentry-Fourchambault & Decazeville fournissent alors une barre fer 60% - nickel 30% au BIPM qui permet à Charles-Edouard Guillaume de constater un coefficient de dilatation thermique environ 4 fois plus faible que celui du fer ou du nickel. Avec le soutien des fonderies Commentry-Fourchambault & Decazeville et de son directeur Henri Fayol qui lui fournit plus de 600 variations de l'alliage Fer/Nickel, il teste alors une large palette d'échantillons contenant diverses proportions de nickel.
Pour chaque alliage il mesure le coefficient de dilatation thermique à diférentes températures grâce à un bain d'huile monté sur une chaudière. Il détermine ansi des relations linéaires donnant pour chaque concentration de nickel le coeficient de dilatation:
α = a + b T
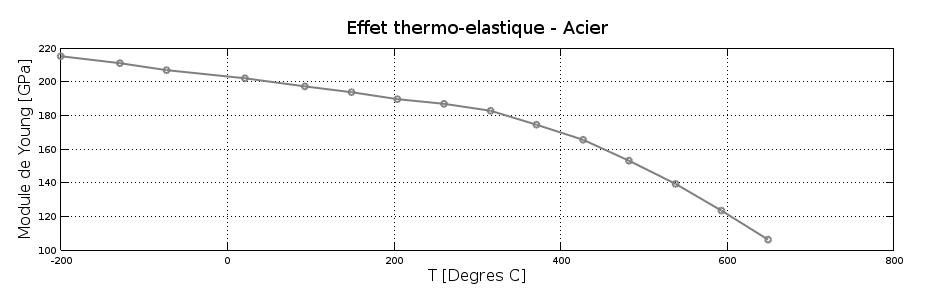
En 1897 il publie un article montrant en particulier que l'alliage comprenant 36% de Nickel possède le coefficient de dilatation le plus faible, largement inférieur à celui du platine iridié (voir graphique ci-dessous). Cet alliage sera nommé Invar par Marc Thury (ingénieur et professeur originaire de Nyon) et il aura des applications immédiates dans la métrologie ainsi que pour la confection de balanciers de pendules.
Etude de Charles-Edouard Guillaume sur l'anomalie de dilatation des aciers au nickel (Guillaume, 1898) [Graphique: www.numeritec.ch]
Applications de l'anomalie de dilatation en horlogerie
Dans sa publication de 1904, "Les applications des aciers au nickel", Charles-Edouard Guillaume liste trois domaines principaux d'utilisation de l'Invar en horlogerie: la tige du balancier de pendule, le balancier de montre, le ressort spiral.
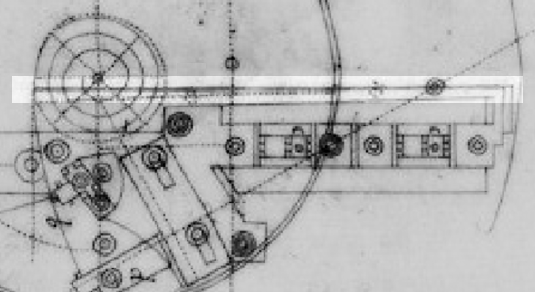
Tige de balancier pour pendule - Guillaume présente une solution utilisant l'invar pour la tige de balancier. La faible dilatation vers le bas de la tige est compensée par la dilatation vers le haut de la lentille grâce à sa fixation en son point bas. Le professeur Thury propose et teste dans les locaux de la Société Genevoise de Physique une construction légèrement différente en ce sens que la lentille est fixée à la tige à l'aide d'une vis de réglage.
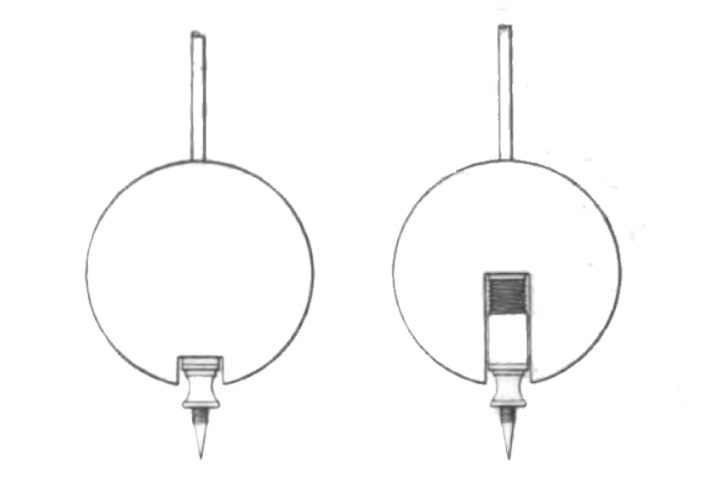
Balanciers de pendule avec tige en invar, proposés par Guillaume (gauche) et Thury (droite).
Guillaume calcule les écarts possibles pour ces deux solutions. Avec le système réglable, qui permet d'ajuster individuellement chaque pendule, il donne une précision de 0,004 secondes par degré et par jour. Sans le système de compensation, en ajustant la construction sur des propriétés moyennes des lots d'invar, la précision prévue est de 0,02 secondes par degré et par jour, ce qu'il estime être largement suffisent pour la plupart des pendules et pour un coût de réalisation très bas.
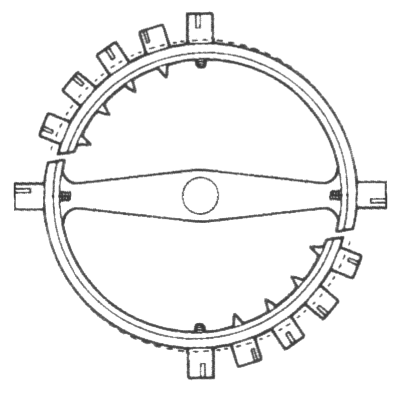
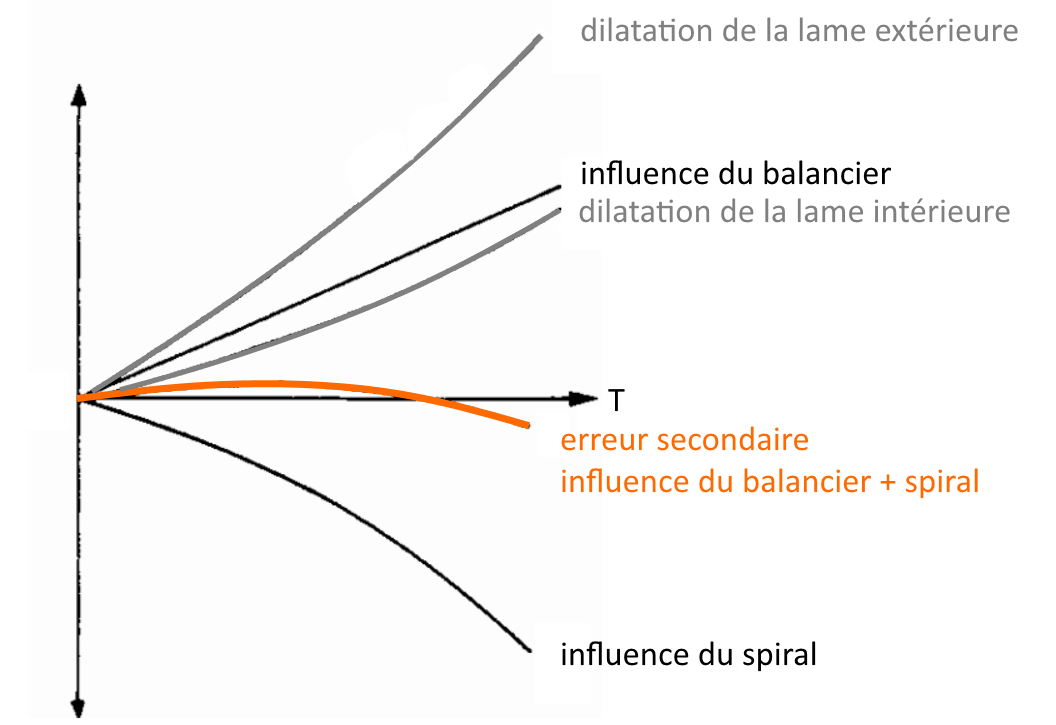
Balancier compensateur - Comme nous l'avons mentionné précédemment, les balanciers bilames acier/laiton ne permettaient pas de corriger l'erreur secondaire. Chalres-Edouard Guillaume a alors étudié la source de l'erreur secondaire et il a proposé une solution en remplaçant la lame d'acier par une lame d'alliage Fer/Nickel judicieusement choisie. Son étude a été publiée dans le Journal Suisse d'Horlogerie en 1899 et elle a suscité l'intérêt de Mr. Nardin au Locle et Mr. Paul Ditisheim à la Chaux-de-Fonds. Tous deux ont souhaité tester ce balancier proposé par Guillaume et c'est Mrs. Ferrier et Vaucher à Travers qui ont réalisé ce balancier.
Les résultats se sont avérés excellents et les systèmes munis du balancier Guillaume - appelé aussi balancier intégral - ont montré une précision dans la compensation des températures inégalée à l'époque.
Spiral - L'exploitation de l'anomalie de dilatation des aciers au nickel pour la fabrication du ressort spiral n'a que peu d'intérêt, en effet la principale source d'erreur n'est pas la dilatation du spiral mais la variation de son module d'élasticité en fonction de la température. Ainsi c'est une autre anomalie qui trouvera un application pour le spiral, l'anomalie d'élasticité.
Anomalie du module d'élasticité des aciers au nickel
En 1897, le professeur Thury donne une conférence à la classe d'Horlogerie de l'Ecole des Arts de Genève, au cours de laquelle il évoque le fait qu'un acier contenant 36% de nickel (invar) présente un module de Young qui augmente avec la température. Cette caractéristique est contraire au comportement usuel du module d'élasticité qui, généralement, diminue lorsque la température augmente. Charles-Edouard Guillaume, qui avait confié à un régleur de la Chaux-de-Fonds, Mr. Paul Perret, un spiral en acier fer/nickel 36%, avait obtenu la confirmation de l'anomalie du module de Young par les essais de ce dernier.
Applications de l'anomalie d'élasticité en horlogerie
En collaboration avec Mr. Perret et les fonderies de Commentry-Fourchambault & Decazeville, Charles-Edouard Guillaume dirige alors une étude dont le but est de découvrir un alliage dont le module de Young serait indépendant de la température.
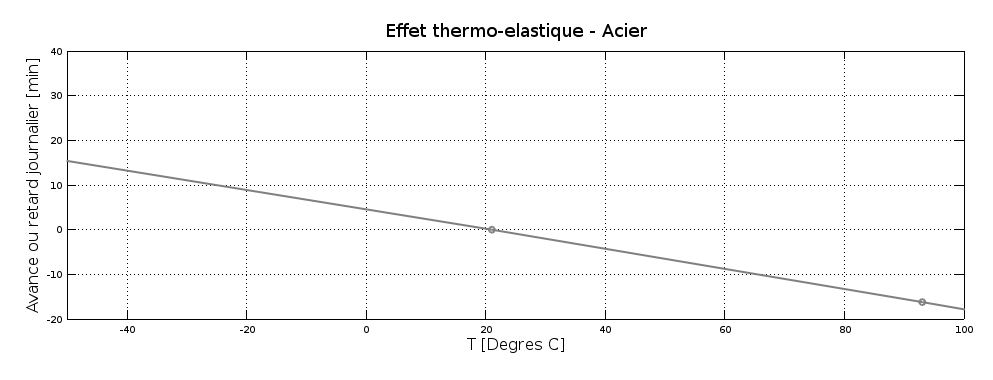
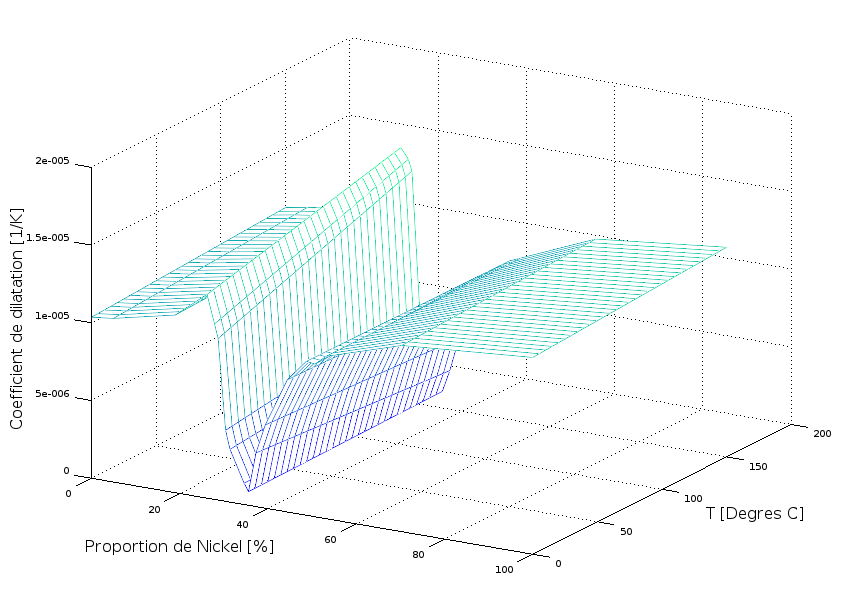
Dans sa publication de 1904, "Les Applications des Aciers au Nickel", Charles-Edouard Guillaume est bref et plutôt mitigé sur l'utilisation d'un alliage au nickel pour la fabrication du ressort spiral. Or, dans le cas de ce composant, la principale perturbation sur la fréquence d'oscillation du système balancier/spiral provient de la variation du module d'élasticité du spiral. Il identifie deux concentrations de nickel qui permettent de produire un alliage dont la variation du module d'élasticité dans une large plage de température est très faible. Il s'agit des variantes à 28% de nickel ainsi que celle à 42% de nickel (cf graphique).
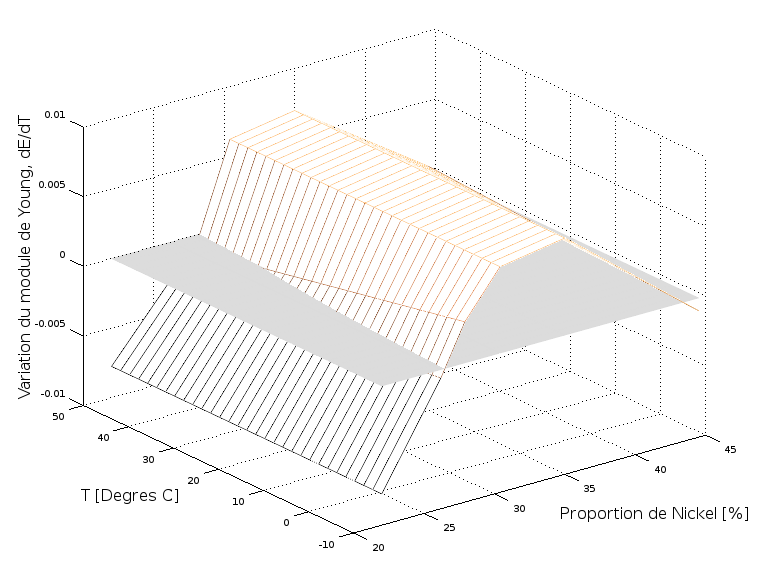
Variation du module de Young (dE/dT) pour différents aciers au nickel (Guillaume, 1904) [Graphique: www.numeritec.ch]
La variante à 42% de nickel présente un inconvénient. Son module d'élasticité est certes quasi-constant, mais il a une valeur basse. Même si, en théorie, le fonctionnement d'un ressort spiral ne s'en trouverait pas altéré, Guillaumes craint des problèmes lors de la manipulation de ces ressorts à faible rigidité et il écarte cette solution.
La variante à 28% de nickel a un module de Young presque constant et sa valeur est plus élevée, c'est un meilleur candidat pour la fabrication des spiraux. Cependant l'erreur secondaire reste importante et d'un point de vue pratique la forte variabilité du module de Young pour des compositions voisines de 28% nickel rendent son utilisation peu intéressante aux yeux de Charles-Edouard Guillaume. Les variations de qualité des lots d'alliage ainsi que les inhomogénéités au sein d'un lot limitent le potentiel correcteur pour ce matériau. Charles-Edouard Guillaume n'y voit d'intérêt que pour les montres bon marché qui ne sont de toute façon pas équipées de balanciers compensateurs, l'écart sur la marche diurne entre 0° et 30° passe de ~6 minutes pour un spiral acier à ~0,5 minute pour un spiral en élinvar. De plus ces aciers au nickel ont une très faible sensibilité aux champs magnétiques, ce qui était un argument que l'on commençait à considérer.
Alliages ternaires
L'ajout d'un troisième composant tel que le manganèse, le chrome, le carbone, etc..., confère à l'alliage des propriétés physico-chimiques qui peuvent servir pour différentes applications pratiques. Le manganèse permet entre autre de faciliter l'utilisation en fonderie, tandis que l'ajout de chrome ou de carbone augmente la limite élastique et s'avère intéressant pour la fabrication de ressorts.
Charles-Edouard Guillame se consacre en particulier à la recherche d'un alliage dont le module élastique serait suffisemment élevé, peu sensible aux inhomogénéités de composition et dont la variation avec la température serait nulle. Dors et déjà il nomme ce futur alliage élinvar pour souligner sa caractéristique principale: son "élasticité invariable".
L'ajout de chrome a non seulement pour effet d'augmenter le module de Young, mais il diminue l'anomalie d'élasticité. En choisissant une proportion de 12% de chrome, le pic d'anomalie dE/dT (cf figure ci-dessus) ne coupe plus le plan "zéro" en deux lignes mais il en devient tangent en son sommet. Ainsi les inhomogénéités de l'alliage n'ont qu'un faible impact sur les caractéristiques "invariables" du matériau.
Le composé Fe58%, Ni36% et Cr12% devient le premier élinvar défini par Guillaume.
Cet alliage a encore été amélioré par les fabricants qui ont ajouté divers composants à durcissement structural (tungstène, béryllium, molybdène,...), donnant les actuels nivarox, métélinvar, durinval, isoval etc...
Ces spiraux auto-compensateur sont utilisés avec des balanciers monométalliques qui sont eux-même stables par rapport aux variations de température. Le matériau le plus répendu aujourd'hui pour le balancier est probablement le glucydur (cf encadré).
Balancier à affixes compensateurs
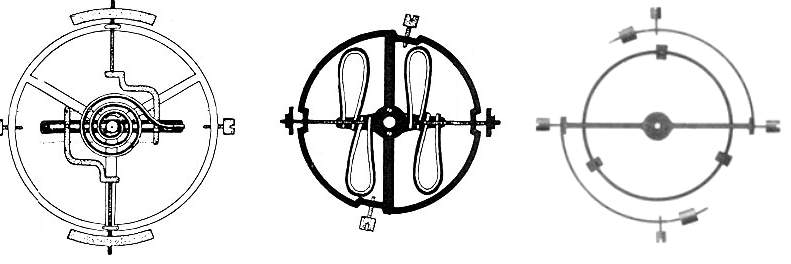
Ce système imaginé par Paul Ditisheim conciste à fixer sur la serge du balancier monométallique deux petits bilames équipés de masses compensatrices que l'on peut déplacer afin de régler l'effet correcteur. Dans la variante Daniels les affixes sont fixés sur les bras du balancier. Ces affixes ne permettent que de faibles compensations, mais ils rendent aux régleurs la possibilité d'ajuster très précisément la marche d'une montre équipée d'un spiral en élinvar et supprimer les erreurs résiduelles.

Balancier à affixes compensateurs Ditisheim
Autres systèmes compensateurs
D'autres systèmes de compensations ont été imaginés par la suite, tels que le balancier différentiel coupé ou le balancier différentiel simple. Ces systèmes utilisent des matériaux diférents pour les bras et la serge du balancier, d'où une différence de coefficient de dilatation qui génère des déformations - ovalisations - que l'on peut ajuster pour compenser l'effet thermique sur le spiral.
Mentionnons également le balancier à serge anisotrope développé par R. Straumann. On obtient une anisotropie du coefficient de dilatation de la serge par laminage. Comme pour le balancier différentiel la conséquence est une ovalisation du balancier lors d'une augmentation de température.